Xác định ly độ, vận tốc và thời gian
- Bài toán cho t tìm x, v, a và ngược lại
Phương pháp.
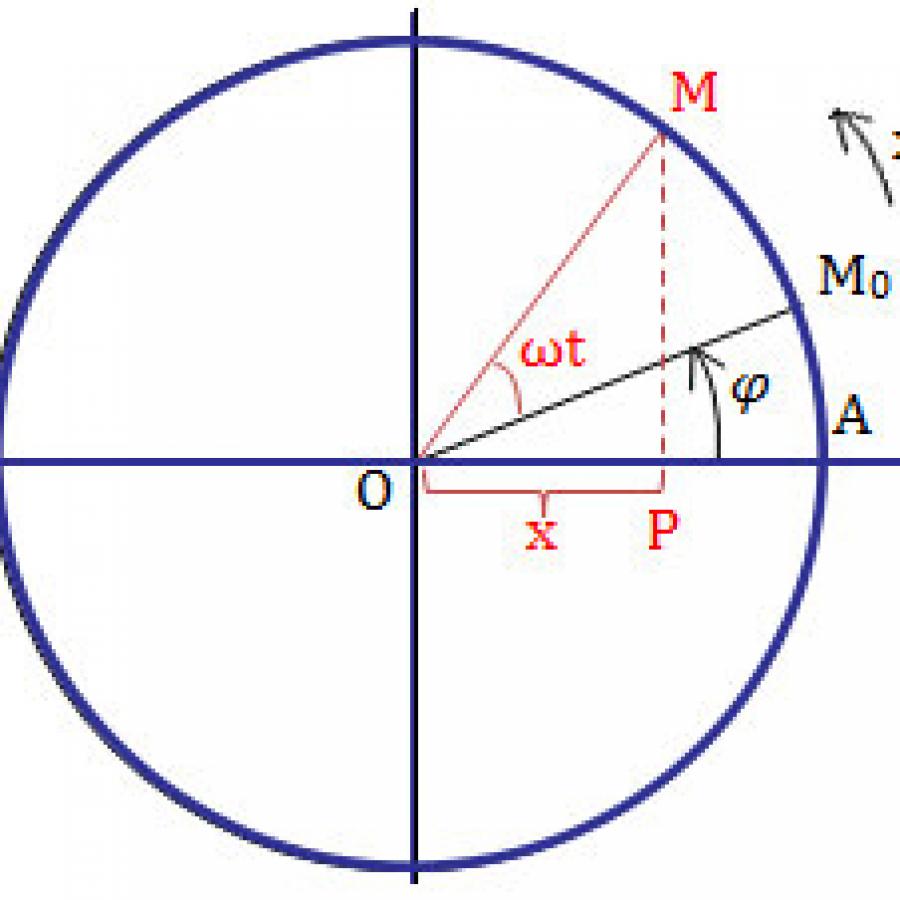
Sử dụng công thức x, v, a theo thời gian t:
$x = Ac{\text{os(}}\omega {\text{t + }}\varphi {\text{)}}$
$v = x’ = – \omega A\sin (\omega t + \varphi ) = \omega Acos(\omega t + \varphi + \dfrac{\pi }{2})$
$a = v’ = – {\omega ^2}A\cos (\omega t + \varphi ) = – {\omega ^2}x$
- Bài tập cho x, v hoặc a tìm các đại lượng còn lại tại cùng một thời điểm.
Sử dụng hệ thức độc lập
– Hệ thức độc lập A-x-v: ${A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}{\text{ }}$
– Hệ thức độc lập A-a-v: ${A^2} = {\dfrac{a}{{{\omega ^4}}}^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}$
– Quan hệ giữa a-x: a=-ω2x
- Bài tập cho x, v hoặc a tại một thời điểm t1 tìm x, v, a tại thời điểm trước (hoặc sau) đó T/4, T/2, 3T/4, …
Biết tại thời điểm t vật có li độ x = x0.
* Từ phương trình dao động điều hoà: x = Acos(wt + j) cho x = x0
Lấy nghiệm wt + j = a với $0 \leqslant \alpha \leqslant \pi $ ứng với x đang giảm (vật chuyển động theo chiều âm vì v < 0) hoặc wt + j = – a ứng với x đang tăng (vật chuyển động theo chiều dương)
* Li độ và vận tốc dao động sau (trước) thời điểm đó Dt giây là
$\left\{ \begin{gathered}{\text{x }} = {\text{ Acos}}( \pm \omega \Delta t + \alpha ) \hfill \\ v = – \omega {\text{A}}\sin ( \pm \omega \Delta t + \alpha ) \hfill \\\end{gathered} \right.$ hoặc $\left\{ \begin{gathered}{\text{x }} = {\text{ Acos}}( \pm \omega \Delta t – \alpha ) \hfill \\ v = – \omega {\text{A}}\sin ( \pm \omega \Delta t – \alpha ) \hfill \\\end{gathered} \right.$