Viết phương trình dao động điều hòa

08/12/2019 , 45.005 views

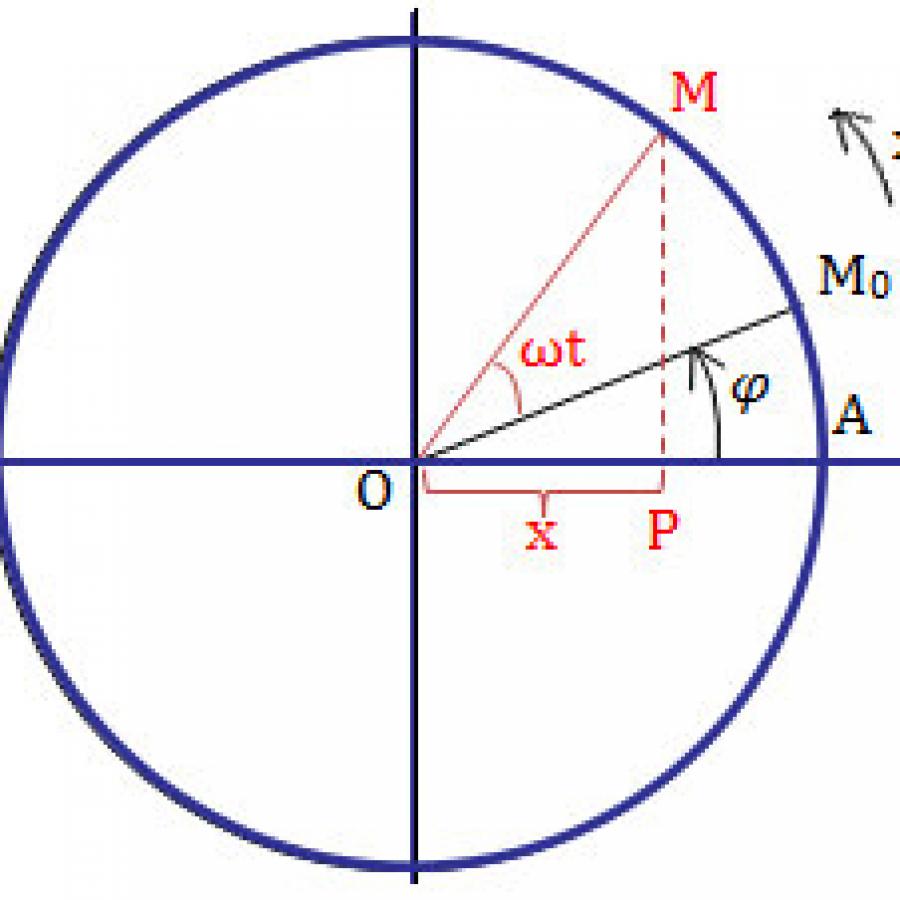
Phương trình dao động tổng quát: $x{\rm{ }} = {\rm{ }}Acos\left( {\omega t{\rm{ }} + {\rm{ }}\varphi } \right)$

– Bước 1: Tìm A: $\left\{ \begin{array}{l}
A = \dfrac{{{v_{{\rm{max}}}}}}{\omega } = \dfrac{{{a_{{\rm{max}}}}}}{{{\omega ^2}}} = \dfrac{L}{2} = \dfrac{S}{4} = \dfrac{{{v_{{\rm{max}}}}^2}}{{{a_{{\rm{max}}}}}}\\
{A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {\dfrac{a}{{{\omega ^4}}}^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}
\end{array} \right.$

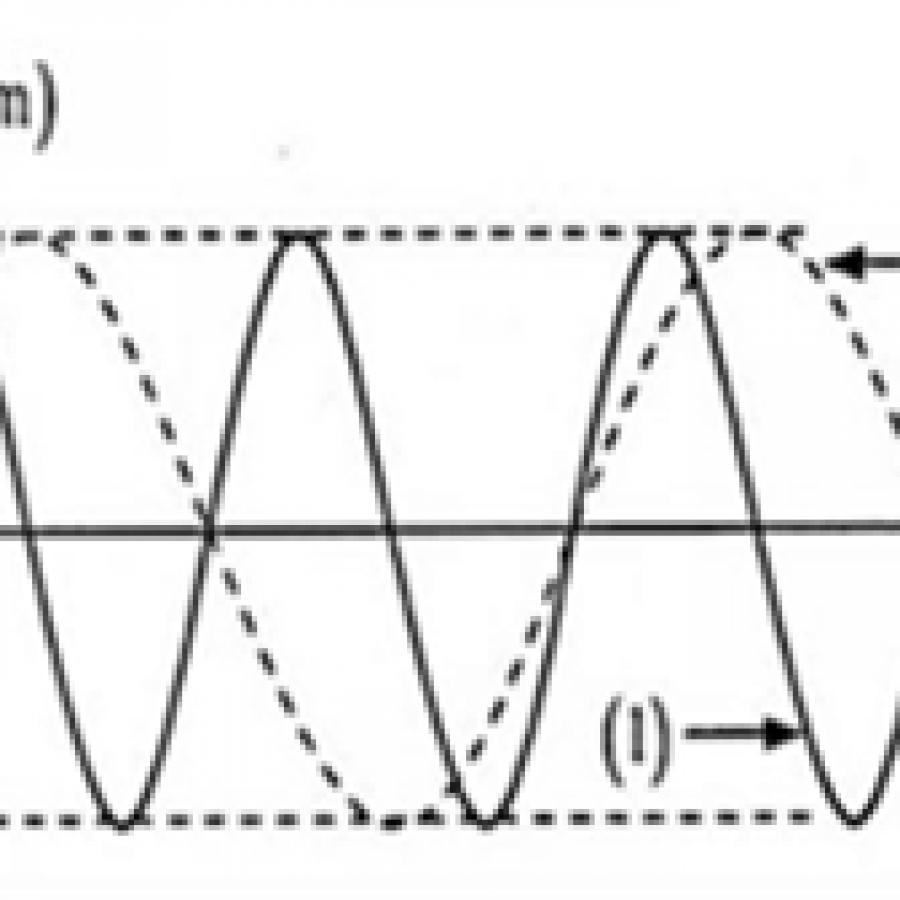
L: chiều dài quỹ đạo của dao động
S: quãng đường vật đi được trong một chu kì

– Bước 2: Tìm Tìm $\omega$: $\omega = \sqrt {\dfrac{k}{m}} = 2\pi f = \dfrac{{2\pi }}{T} = \sqrt {\dfrac{{{a_{{\rm{max}}}}}}{A}} = \dfrac{{{v_{{\rm{max}}}}}}{A} = \dfrac{{{a_{{\rm{max}}}}}}{{{v_{{\rm{max}}}}}} = \sqrt {\dfrac{{{v^2}}}{{{A^2} – {x^2}}}} $

Trong đó:

Chu kì T: $T = \dfrac{t}{N}$
Tần số f: $f = \dfrac{N}{t}$
N là số dao động vật thực hiện được trong khoảng thời gian t

– Bước 3: Tìm $\varphi $

Tại t = 0: $\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi \\{\rm{v = – A}}\omega {\rm{sin}}\varphi \end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\dfrac{{{x_0}}}{A}\\\sin \varphi = – \dfrac{v}{{A\omega }}\end{array} \right. \to \varphi = ?$